結城浩
2003年3月26日
長男とお風呂。
長男「ねえ、クイズだして!」
私「じゃあ、3つの数を順番にいうから、4つめの数をあてるんだよ。」
長男「うん」
私「0, 0, 0, 次は?」
長男「0。簡単」
私「じゃあ、1, -1, 1, 次は?」
長男「-1。簡単」
私「どうして-1なの?」
長男「だって(といって指を出し)1でしょう。そしてぴょんと-1でしょう。でぴょんと1だから、次は-1」
私「ふんふん。じゃあねえ。1000, 100, 10, 次は?」
長男「次は、1。簡単だよ」
私「じゃあ、その次は?」
長男「え? 1000, 100, 10, 1, その次は…0かな。いやいや。10分の1だ」
私「その通り。賢いねえ」
長男「へへ」
私「10分の1の代わりに0.1といってもいいね」
長男「10で割っていくんでしょ」
私「その通り。小数点を1つずつ左に動かしていくといってもいい。1, 2, 6, 24, 次は?」
長男「ええ?…6の次が42だったらわかるんだけど…」
私「ふうん。どうして?いってごらん?」
長男「1でしょ。1の次の数の2をかけると2になる。2の次の数の3をかけると6になる。6の次の数の7をかけると42だから」
私「それは、とてもとっても面白いねえ。なるほど。でも、私の問題の答えではない」
長男「1, 2, 6, 24, …難しいなあ」
私「ところでさっき、どうして「掛け算」が出てきたのかな」
長男「あのね。何だか急に大きくなってたから。足し算だとそんなに大きくするのは難しいでしょ」
私「あなたは賢いねえ。それは大きなヒントだ」
長男「うーん。…わかんない」
私「1に2をかけたら2, 2に3をかけたら6, 6に4をかけたら24, だから、2, 3, 4を順にかけている。だから次は24×5で120」
長男「なるほどー。ねえお父さん。このクイズって、答えは1つしかないの」
私「そんなことはないよ。たとえば1, 2, 6, 24, の次に100万という答えだって作れる。でもそのときの規則はあまり面白いものではない。『うん、確かにそうだね』という規則を見つけることが面白いんだ。じゃあ次ね。1, -2, 6, -24, 次は?」
長男「(笑って)おんなじじゃん」
私「数の列は違うよ」
長男「次は120でしょ」
私「その通り。どうしてそう思ったの?」
長男「さっきと同じだけど、マイナスになって、マイナスじゃなくて、というのが繰り返すから」
私「そうだね。それは「符号が変わる」っていうんだ。プラスとマイナス」
長男「フゴウ? フトウシキっていうのもあるね」
私「うん。でも不等式のフと符号のフとは字が違う。不等式は等式じゃないというフだ。2つの数aとbがあるとしよう。不等式は4通りある」
長男「え?「aはb以上」「aはb以下」…それから?」
私「「aはbより大きい」「aはbより小さい(未満)」」
長男「あ、そうだね。「より大きい」って別の言い方はないの?」
私「ないねえ。でも、英語はもっと大変なんだよ。「以上」「以下」っていう簡潔な言い方はなくて、「greater than or equal to」「less than or equal to」になっちゃう。」
長男「ふうん」
私「じゃあクイズね。ある数は100以上で100以下です。この数は何ですか」
長男「うーんと、100」
私「はい、正解です。じゃあ、ある数は100以上で100未満です。この数は何ですか」
長男「そんな数はないよ」
私「はい、正解です」
長男「(笑う)」
私「マジシャンが言いました。『何か数を思い浮かべてください。その数を当てます。あなたが思った数は【100以上かまたは100未満】ですね!』」
長男「(大笑いする)あったりまえじゃん!」
私「そうだね。ところで、そのマジシャンの話を聞いた間抜けなマジシャンがまねをして言いました。『何か数を思い浮かべてください。その数を当てます。あなたが思った数は【100より大きいかまたは100未満】ですね!』」
長男「あはは」
私「そう。相手が100を考えたので外れてしまいましたとさ。ところで「100以上かまたは100未満」っていう話を聞いたとき、あなたはどんなことを考えた?」
長男「あのね。(湯煙でくもる鏡に指で直線を描く)こうあって、ここが100で、「100以上」っていうと、ここも入れて右でしょ(シュッ)。「100未満」だと、ここを入れないで左(シュッ)」
私「そうだね。その通り。入れるか入れないかをはっきりさせるために、黒丸白丸を使うこともある。100以上なら、100のところを黒丸にして右にシュッ。100未満なら100を白丸にして左にシュッ」
長男「なるほどね。黒丸は「そこ」を入れるんだ」
私「その通り。ところで、またマジシャンだ。ある人がマジシャンを負かそうとやってきた」
長男「ふんふん」
私「マジシャンが言いました。『何か数を思い浮かべてください。その数を当てます。あなたが思った数は【100以上かまたは100未満】ですね!』すると、相手は「いいえ、違います。私が考えた数は『2乗したら-1になる数』ですから」と答えた」
長男「え?2乗したら-1?そんなのあるの?」
私「あります。2回かけたら-1になる数。あります」
長男「存在しないよ」
私「存在します。たとえばあなたは1という数が存在すると思う?」
長男「存在するよ。整数でしょ?」
私「うん。そうだね。あなたが1という数が存在すると思うのと同じ程度に、2回かけたら-1になる数も存在すると言える。普通はその数にi(アイ)と名前をつける。虚数単位とも言う」(※実際には-iも二乗すると-1になります)
長男「-1は二乗すると?」
私「1になる」
長男「1は二乗すると?」
私「1になる」
長男「じゃあ、やっぱりiなんて数は存在しないよ」
私「多くの人がそう考える。そして想像上の数としてiという名前をつけた。でも存在する。見せてあげよう」
長男「うん!」
私「(鏡に指で数直線を描く)ここを0として、ここが1、ここが-1としようね」
長男「うん」
私「(指で指しながら)1に-1をかけると、-1になる。-1に-1をかけると1になる。2に-1をかけると-2になる。-2に-1をかけると2になる」
長男「そうだね」
私「何かに-1をかけると…(指で指しながら)ぴょんと符号が変わる」
長男「うん」
私「ということは、「-1をかける」というのは「180度ぐるっとまわす」ことなんだ」
長男「そうだね!」
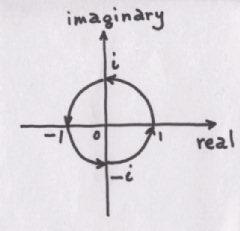
私「そこで、iという数は「90度まわす」ことだと考えてみよう。そうすると、iを二回かけると-1をかけたことと同じになる」
長男「…!」
私「すると、さっき描いた数直線に直角に交わる縦の数直線を考えることができる。交点は0。横が「実数」の数直線。縦が「虚数」の数直線だ。虚数は実数の数直線上にないから、実数と比べることができない」
長男「ふうん…」
私「だからiは、100以上でもなく、100未満でもない」